Communeの社内コミュニティのデータを使ってネットワーク分析の基礎を学ぶ

データ

こんにちは、Communeのデータサイエンティストの樋口です！

Communeでは、"あらゆる組織とひとが融け合う未来をつくる"のミッションのもと、組織とひととのつながりを支えるコミュニティサクセスプラットフォーム「Commune」を開発しています。

Communeでは人のつながりを科学し、プロダクトを利用するお客さんが再現性を持って活発なコミュニティを作れるように尽力しています。

本ブログではその取り組みの一環として、表形式よりも人のつながりを柔軟に表現できるネットワークを用いて、オンラインにおけるコミュニケーションパターンの分析を実施したので、記事にしてみました！

Communeのデータを使った具体的な分析事例を元に、ネットワーク分析の基本的な知識を学び、コミュニティサクセスに役立つ洞察を探っていきます。

今回のブログに利用したコードはクエリなどを除き、Gistに公開しているので、併せて参照ください。

ネットワーク分析の基礎知識

まず、ネットワーク分析の基礎知識について紹介します。

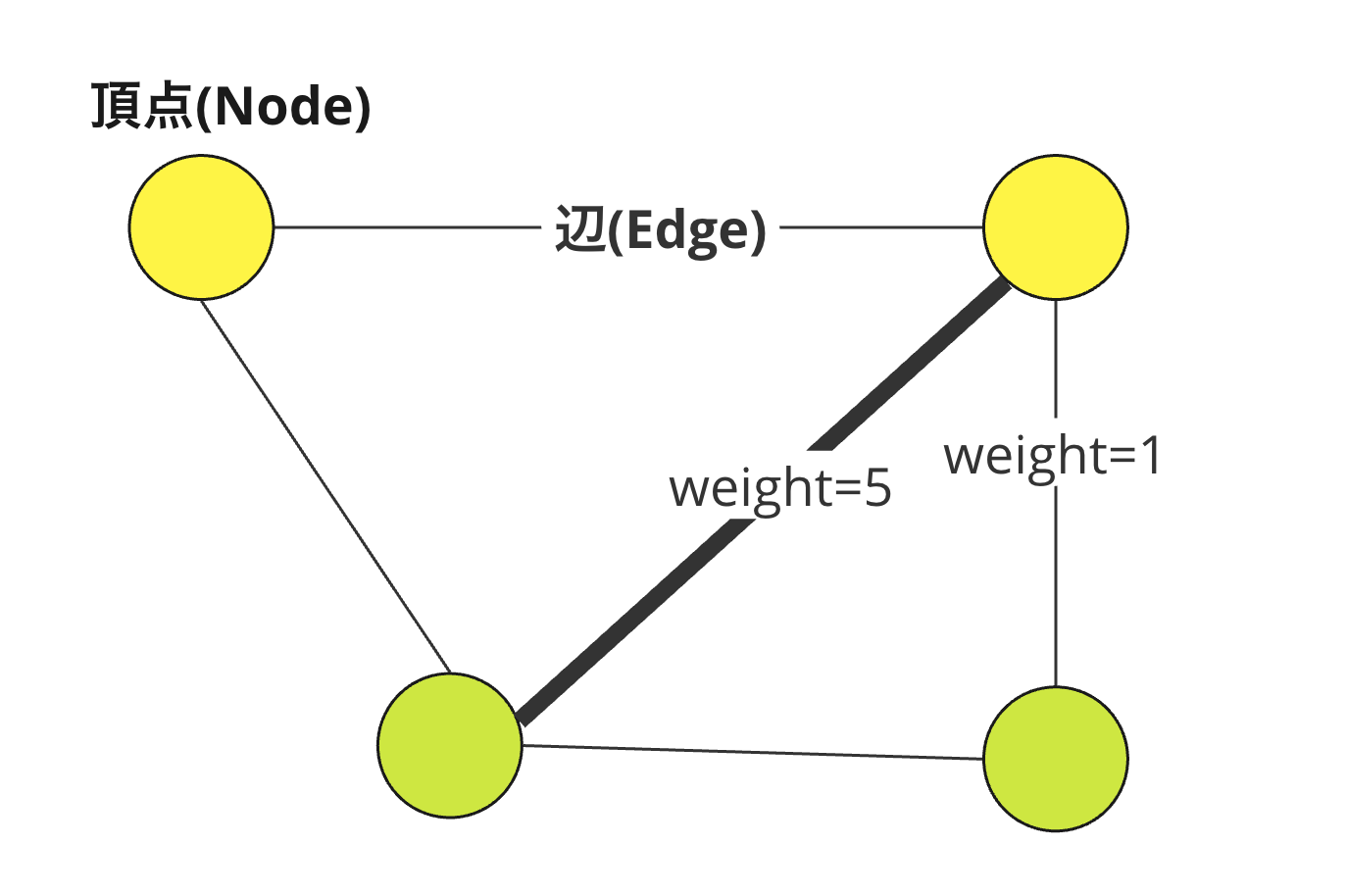
ネットワークとは、物事の関係性を頂点（ノード）と辺（エッジ）で記述するデータ構造のことです。この構造は、道路や人のつながり、化合物など様々なものを柔軟に表現できます。

ネットワークは頂点や辺に属性(グループや辺の重みなど)を定義することや、辺に方向性を持たせることも可能です。

プログラミングでネットワークを定義する場合は隣接行列や辺リストを用いて表現します。

# 隣接行列
    A B C D
  ---------
A | 0 1 1 1
B | 1 0 0 1
C | 1 0 0 1
D | 1 1 1 0

---
# 辺リスト(重み付き)
(A, B, 1)
(A, C, 2)
(A, D, 3)
(B, D, 4)
(C, D, 5)

ネットワークの分析と一口に言っても、多様なアプローチがあり、下記のように様々な視点から分析することができます。

  • 森（全体俯瞰）:
    • ネットワーク可視化したり、クラスタ係数といった特徴量の計算を行い、ネットワークの全体の特徴や傾向をつかむ
  • 林（中間レベル）:
    • クラスタリングを行ったり、経路上のボトルネックを特定し、ネットワーク内の特徴となる経路やグループを見つける
  • 木（個別の特徴）:
    • 個々のノードに注目し、働きかける分析。
    • 将来の友人関係の予測や、口コミ情報の伝搬促進・抑制を行ったり、ネットワークの中で中心的な存在となる頂点を同定する など

人と人のコミュニケーションは相互作用によって成り立っています。

この相互作用を考慮する場合、表形式よりもネットワークを用いた方が柔軟に表現でき、コミュニケーションパターンや構造をより明確に把握することができると考えています。

「Marble」と今回使うデータセットの説明

次に、今回の分析で使うデータセットを紹介します。

社内では、プロダクトの理解とオンラインコミュニケーションを促進するために、Communeを活用したコミュニティ「Marble」を運営しております。今回はこのコミュニティのデータを利用しようと思います。

MarbleはCommune社内のインフォーマルなコミュニケーション活性のためのコミュニティで、投稿や社内イベントなどが掲載されています。

各投稿では、このようにコメントのやりとりができます。

今回はこのコメントのやりとりがある人同士を交流があると見なし、エッジを張ることでネットワークを形成していきます。

下記のような、クエリで両者間のコメント回数を重みとした無向グラフを形成します。

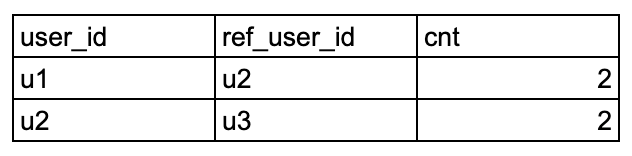
クエリ

with comment_edges as (
    select 
      c.comment_id,
      du1.user_id,
      du2.user_id as ref_user_id
    from comments as c
    left join dim_users as du1 on du1.user_id = c.user_id
    left join dim_users as du2 on du2.user_id = c.ref_user_id
),
normalized_edges as (
    select 
        least(user_id, ref_user_id) as user_id, 
        greatest(user_id, ref_user_id) as ref_user_id,
        count(distinct comment_id) as cnt
    from comment_edges
    group by 1,2
    order by cnt desc
),
final as (
    select 
        ne.user_id, 
        ne.ref_user_id,
        du1.display_name as user_name,
        du2.display_name as ref_user_name,
        ne.cnt
    from normalized_edges ne
    left join dim_users du1 on ne.user_id = du1.user_id
    left join dim_users du2 on ne.ref_user_id = du2.user_id
)
select * from final

NetworkX

ネットワーク分析にはPythonのNetworkXを用います。NetworkXはネットワーク分析を行う時に、ネットワークを直感的かつ簡単に扱えるライブラリです。

下記のように、取得したデータをTupleで格納することで、エッジを登録し、ネットワークを構築することが出来ます。

import networkx as nx
G = nx.Graph()
edges = raw_df.select(["user_name", "ref_user_name", "cnt"]).to_numpy()
G.add_edges_from((u, v, {"weight": w}) for u, v, w in edges)

具体的な解析については以降の章でコード含め、解説します。NetworkXの文法は公式のTutorialが網羅的に記載されているので、詳しく知りたい方におすすめです。

networkx.org

ネットワーク分析

統計量

まずはネットワークの全体像をつかむために、ネットワークの統計量を確認します。 ネットワークの特性を見るために､ここでは密度、平均次数、平均経路長を計算しています。

密度はグラフがどれだけ密にエッジで結ばれているかを示す指標で、実際のエッジ数 / 可能な最大エッジ数で算出します。

$$ \text{Density} = \frac{2|E|}{|V|(|V| - 1)} $$

  • $|E|$: グラフのエッジ数（辺の数）
  • $|V|$: グラフのノード数（頂点の数）

次数は、各ノードに接続しているエッジの数を示す指標で、全ノードの平均で平均次数が割り出せます。

$$ \deg(v) = \left| { u \in V : (u, v) \in E } \right| $$

$$ \bar{k} = \frac{1}{|V|} \sum_{v \in V} \deg(v) $$

  • $(u, v)$: ノード $u$ からノード $v$ へのエッジ
  • $V$: グラフのノードの集合
  • $E$: グラフのエッジの集合

経路はグラフのノード間において一連のエッジのことを指します。平均経路長はグラフ内の全てのノードペア間の最短経路長を計算し、それをノードペアの総数で割ったものです。平均経路長が短いほど、ノード間の通信や情報の伝達が効率的であることを示します。

$$ \bar{L} = \frac{1}{|V|(|V| - 1)} \sum_{u, v \in V, u \neq v} d(u, v) $$

  • $d(u, v)$: ノード $u$ からノード $v$ への最短経路長
  • $\sum_{u, v \in V, u \neq v}$: 全ての異なるノードペア $(u, v)$ についての総和

NetworkXではそれぞれ、下記のように計算することができます。

num_nodes = G.number_of_nodes()
num_edges = G.number_of_edges()
density = nx.density(G)
avg_degree = sum(dict(G.degree()).values()) / num_nodes
average_path_length = nx.average_shortest_path_length(G)

このネットワークはノード数(V) = 120, エッジ数(E)= 405, 平均次数6であり、密度が0.05と低く、平均経路長2.5と短いです。

このような密度が低く、平均経路長が短いネットワークは「スモールワールドネットワーク」と呼ばれます。現実の知人関係を表すネットワークは、このスモールワールドネットワークの特性を持ちやすいです。

Marbleのデータセットも例に漏れずこの形状を持っているということになります。

スモールワールドネットワークは、局所的には高いクラスタリング係数を持ちつつ、全体的には短い経路長を特徴とするネットワークであり、効率的な情報伝達と強いコミュニティ構造の両方を兼ね備えています。

kotobank.jp

次数分布

次に、ネットワークの次数分布を確認します。次数分布は、各ノードの次数（他のノードと接続しているエッジの数）がどのように分布しているかを示します。

degree_sequence = [d for n, d in G.degree()]
plt.figure(figsize=(10, 6))

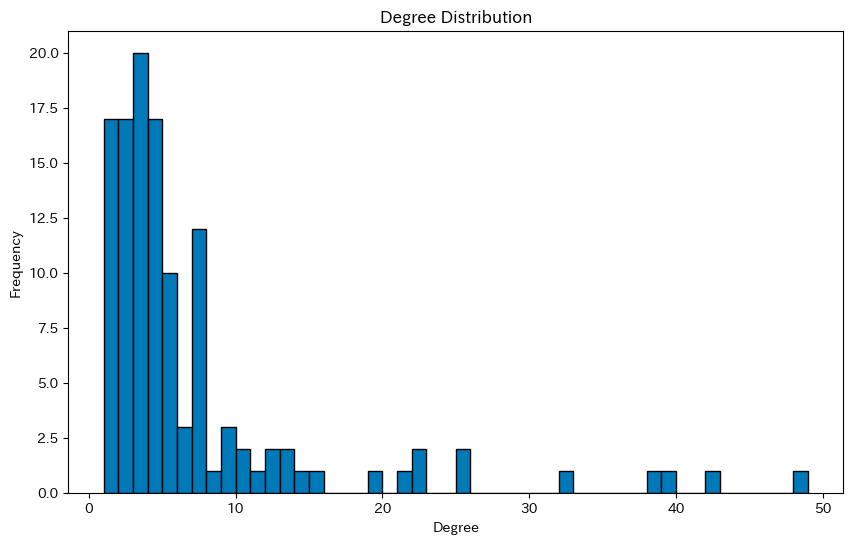
次数分布を見ると、多くの次数を持っている少数のノードがあり、べき乗分布に近い形をしていることがわかります。

$$ P(k) \propto k^{-\gamma} $$

人のコミュニケーションや航空網といった多くの実ネットワークはこのべき乗分布に従うことがわかっており、このようなネットワークをスケールフリー・ネットワークと呼びます。

次数分布を対数変換し、線形回帰した傾きを用いることで、簡単にγを算出することが出来ます。

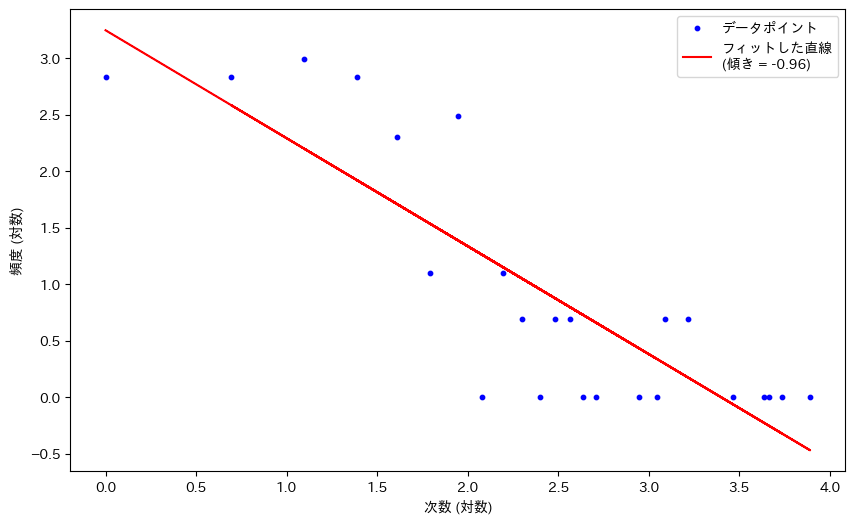
このネットワークではγ=0.96となりました。

一般的にスケールフリー・ネットワークは 2<γ<3であることが多く、Marbleのコメントによるネットワークは相対的に右裾が薄い = 多くの人がコミュニケーションしていることがわかります。

クラスタリング

次にネットワークのノード(ユーザー)をクラスタリングしてみます。クラスタリングを行うことで、様々な示唆を得たり、新たな活用ができます。

  • ネットワークを粗視化することができる
  • 頂点の類別ができる
  • 後から名前をつけたり、グルーピングして処理することができる
  • ネットワークを階層構造で扱うことができる

今回は、モジュラリティ最適化という手法でクラスタリングを行います。 なお、ネットワーク分析の分野では、ノードのクラスタリングのことをコミュニティ抽出とも言います。

モジュラリティ

モジュラリティQはネットワーク内のコミュニティ構造を定量化する指標です。高いモジュラリティ値は、ノードが密に接続されたコミュニティ内にあり、コミュニティ間の接続が少ないことを示します。この値は0~1の範囲をとります。

次のように定義されます：

$$ Q = \frac{1}{2m} \sum_{ij} \left[A_ij - \frac{k_i k_j}{2m}\right] \delta(c_i, c_j) $$

  • $A_{ij}$ はノード $i$ と $j$ の間のエッジの有無（隣接行列）。
  • $k_i$ はノード $i$ の次数。
  • $m$ はネットワーク内のエッジの総数。
  • $c_i$ はノード $i$ が属するコミュニティ。
  • $\delta(c_i, c_j)$ は $i$ と $j$ が同じコミュニティに属している場合に1、異なる場合に0となるクロネッカーのデルタ関数。

A_{ij} - \frac{k_i k_j}{2m} において、同一コミュニティ内でエッジが密で、コミュニティ外のエッジが少ないほど、第二項が小さくなり、$\delta(c_i, c_j)$で1のフラグが立っているときに正の値を取るようになるため、値が大きくなります。

ランダムにコミュニティを初期状態として配置し、貪欲法で解くか、ラグランジュ未定乗数法を用いて、スペクトラルな最適化を使うことができます。

NetworkXでは下記のように簡単に実行することが可能です。

from networkx.algorithms.community import greedy_modularity_communities
communities = greedy_modularity_communities(G)

可視化

上記のクラスタリングをしたネットワークを可視化してみましょう。pyvisを使うことで、インタラクティブな可視化ができます。

pyvis.readthedocs.io

ネットワークの可視化には様々な要求があります。

  • 交差や頂点の重なりを小さくしたい
  • 頂点が平面で散らばってほしい
  • 関連性のある頂点は近くに配置したい
  • 対称性・階層性を反映したい

これらの要求が背反するケースもあるため、目的に応じて可視化方法を選択し、ノードやエッジを配置できると良いでしょう。

今回は、ノード全体に斥力・エッジがある部分は引力を働かせることでなるべく関連性があるノードを近づけつつ頂点の重なりを減らすように可視化をしています。

pyvisではBarnes-Hut法という相互作用の計算方法を用いることで計算量のオーダーを減らしつつ上記の可視化を実現しています。

computing2.vdslab.jp

実装としては、NetworkXで定義されたnodeやedgeやそれらの属性(weightや色)などをpyvisのNetworkに渡すことで実現できます。

from tqdm import tqdm
from pyvis.network import Network

communities = nx.community.greedy_modularity_communities(G)

color_map = {}
colors = ["red", "blue", "green", "purple", "orange", "yellow", "brown", "pink"]
for i, community in enumerate(communities):
    color = colors[i % len(colors)]
    for node in community:
        color_map[node] = color

net = Network(notebook=True, cdn_resources="in_line")

for node in G.nodes():
    net.add_node(node, label=node, color=color_map[node])

for edge in tqdm(G.edges(data=True)):
    net.add_edge(edge[0], edge[1], value=edge[2]["weight"])

net.show_buttons(filter_=["physics"])
net.show("marble3.html")

また、html上のバーを使ってパラメータや計算方法を変更することも可能です。

可視化の考察

ネットワークを見ると、同一コミュニティ内のエッジは密で､それ以外は疎になっており、確かにうまく分割されていることがわかります。

ネットワークのノードにユーザ名を表示できます。ユーザ名と照らしながら、ネットワークの構造や、エッジの太さを観察することで下記のようなことがわかりました。

  • Marble運営チームは多くのユーザに対してエッジが張られており、コミュニケーションのハブになっている
  • 部活動チームや部署など、リアルでのコミュニケーションが頻繁なサブグループと、ネットワーク上のクラスタリングの分類も概ね一致している
  • コアなユーザ同士のエッジのウェイトが特に強く、頻度高く交流しいることがわかる

コミュニティサクセスへの活用

ここまで分析し、コミュニティの活動を表形式のデータではなく、相互作用を持つネットワーク構造にして扱うことでコミュニティサクセスのためにできることの幅が更に広がりそうだなと感じました。

例えば、中心性といった指標を用いて影響力の高いユーザーを特定し、特別な役割や権限を付与することでコミュニティ内の活動を促進できます。

また、モジュラリティ最適化を用いてサブグループを特定し、サブグループごとにイベントやプロジェクトを企画することで、グループ内の結束を強化することもできそうです。

さらに動的ネットワーク分析を使って時間の経過とともにコミュニケーションパターンの変化を追跡することで、コミュニケーションが減少しているサブグループやメンバーにフォローアップや、サポートを提供するなどもできるかなと思いました。

他にも、グラフニューラルネットワークを用いて、ネットワーク構造を考慮したコンテンツのレコメンドや、複数のコミュニティのグルーピングなど様々な活用方法がありそうです！

まとめ

Communeのデータを使ったネットワーク分析について解説してきました。

今回初めてちゃんとネットワーク分析について調べて、集計してみたのですが、Communeには、大小様々なコミュニティがあり、それらのネットワーク特性を理解し、活用することでプロダクトのコアな体験を改善できそうだなという実感をもてました💪

今回は基礎的な分析を紹介しましたが、まだまだ分析・活用できそうなことが多いので今後さらに進展があれば、またブログで報告 & プロダクト改善に活用したいと思います！

参考書籍

複雑ネットワーク : 基礎から応用まで

Pythonで学ぶネットワーク分析 ColaboratoryとNetworkXを使った実践入門